
1win Официальный сайт
Кэшбек до 30%
Хватит искать, где бы сыграть в игровые автоматы или делать ставки на спорт. 1win официальный сайт – лучший портал, если речь заходит об зарате!

И это лишь небольшой перечень, почему вам стоит остановить свой выбор именно на нас. Ведь кроме всего этого, у нас есть уникальная система лояльности, отличные бонусы с хорошими условиями и несколько уровней безопасности.
Компания 1win online начала предоставлять свои услуги еще в 2016 году, и изначально работала под другим названием – First Bet. Азартная платформа быстро обрела популярность, а ее бонусное предложение, которое не свойственно молодым игрокам на рынке — 500% приветственного бонуса, стало привлекать внимание все большего количества пользователей.
Пользователей привлекает не только выгодный бонус за регистрацию, но и различные специальные предложения, а также турниры, которые проходят довольно часто. Заманчивые бонусные программы позволяют зарабатывать неплохие деньги.
| ✅ Минимальный депозит | 100 грн |
|---|---|
| ✅ Минимальный вывод | 1 грн |
| ✅ Минимальная ставка | 20 грн |
| ✅ Средняя маржа | 3-4% |
| ✅ Видеотрансляция матчей | Есть |
| ✅ Онлайн-чат | Есть |
| ✅ Мобильная версия | Android и iOS |
| ✅ Год основания | 2016 |
| ✅ Лицензия | Кюрасао |
От того, насколько надежный ресурс во многом зависит число его клиентов. Поэтому общее количество наших клиентов как никто другой подтвердит вам, что 1win официальный сайт достаточно надежен и безопасен. Мы стараемся удовлетворять все запросы пользователей, чтобы они чувствовали себя защищенными, гарантированно получали выплаты, а их средства были в безопасности. Чтобы убедится в этом, рекоменжуем перейти в раздел «1win отзывы» и убедится в этом самостоятельно!
Учитывая все отзывы о букмекере, можно сделать выводы, что нам доверяют, а число игроков на сайте является тому подтверждением. Положительный имидж компании создает сотрудничество с разными спортивными организациями. Это вызывает лояльное отношение к one вин не только со стороны партнеров, но и пользователей.
Благодаря протоколам шифрования SSL и TSL, все транзакции надежно защищены от хакеров и мошенников. Казино 1 вин также лояльно относится к игрокам, которые применяют специальные стратегии в игре и различные методики – это не запрещено, а значит, разрешено!
Портал имеет понятный на интуитивном уровне интерфейс. Прежде всего, он выполнен в минималистичных тонах, благодаря чему не отвлекает от геймплея. Все необходимые разделы можно увидеть в верхней части интерфейса. А больше дополнительной информации, включая техническую поддержку – в нижней. Благодаря такому разделению, можно легко и быстро найти желаемую категорию.
Некоторые разделы, представленные на ресурсе, пользуются особенно повышенным спросом. А потому они вынесены на самое видное место. Предлагаем подробнее разобраться в том, что они собой представляют.
В нижней части экрана можно найти информацию о бонусах, платежных системах, официальные соцсети, а также ознакомится с правилами пользования сайтом и политикой конфиденциальности.
Помимо того, что наша платформа специализируется на играх на деньги, мы найдем, чем удивить бетторов! У нас представлен обширный выбор спортивных дисциплин, на которые можно сделать ставку. При этом, в отличие от других порталов, у нашей конторы достаточно низкая маржинальность. Она формируется, зависимо от самой дисциплины, а в среднем составляет 6-7%. А какие-либо скрытые платежи или комиссии отсутствуют.
В ассортименте представлены десятки спортивных направлений, на которые можно сделать ставку. Для того, чтобы присоединиться к событию, достаточно сделать минимальную ставку. Это может быть ординар, экспресс или серия. Также бетторы могут наблюдать за развитием событий благодаря трансляции в HD качестве.
Киберспорт — это сравнительно новое, однако популярное направление. Оно отличается от классических спортивных дисциплин, например, футбола или тенниса. В первую очередь, потому что киберспорт – это дисциплина, в которой геймеры соревнуются друг с другом. А вместо классического инвентаря, киберспортсмены используют компьютерное оборудование. Причём по стоимости оно не уступает стоимости других спортивных команд.
У нас в каталоге присутствует довольно широкий выбор компьютерных игр, в которых можно сделать ставку. Среди них отметим самые популярные дисциплины:
БК 1win всегда стремится предложить своим клиентам наиболее выгодные коэффициенты, часто поддерживая маржу всего в 3-4% для значимых спортивных событий. Это обеспечивает беттерам высокие коэффициенты и привлекает все больше пользователей. Официальный сайт Ван Вин доступен для проверки текущих коэффициентов. Кроме того, для некоторых видов спорта мы предлагаем особенно привлекательные коэффициенты, что может привести к выигрышам со значительными суммами при опытной игре.
1win казино не менее популярный раздел на сайте, чем букмекерские ставки. Всё это благодаря тому, что наш портал предоставляет самый большой выбор игровых автоматов среди всех онлайн казино Украины.
У нас вы найдёте более 120 провайдеров со всего мира, среди которых как матёрые представители iGaming индустрии, так и совсем новые. Кстати, одним из самых ярких новичков среди провайдеров, является компания 1win games, которая активно разрабатывает и выпускает онлайн игры совершенно нового формата и высокого уровня качества. Как вы уже догадались по названию, это провайдер от компании 1win, поэтому его игры можно найти только у нас на сайте. Так что заходите скорее и играйте в то, чего больше нет нигде!

Естественно, что наиболее обширный выбор пользователи найдут в категории «1win слоты». Именно здесь сосредоточено более 8 тысяч игровых автоматов. А в категории «Виртуальные игры» пользователи найдут любимую всеми игру 1win Aviator. Обратите внимание, что для удобства эта игра, а также другие мегапопулярные игры на нашем сайте, такие как Lucky Jet, Speed & Cash и другие, закреплены в верхней части сайта. Благодаря чему вы легко можете вернуться к любимым играм с любой страницы сайта.
Согласитесь, что часто достаточно тяжело определиться с тем, во что вы хотите поиграть, но 1win всегда старается угодить своим пользователям и ищет максимально разнообразные способы это сделать. Конечно, библиотека слотов 1вин всегда пополняется новыми автоматами от крупных разработчиков софта, но почему бы не попробовать сделать качественно самим? Этим вопросом задались и разработчики 1 вин и решили порадовать игроков уникальными слот-машинами, где они могут с удовольствием проводить свое свободное время.
Давайте познакомимся с некоторыми слотами производства 1win, после чего вы сможете выбрать один из них и попытать свою удачу там! Начнем?
Выбирайте один из слотов от 1 win казино, чтобы провести свободный вечер в приятной компании с внушительными выигрышами в онлайн казино!
Для тех, кто считает себя ассом в покере, теперь существуют не только известные покер-румы, но и быстро набирающий покер-рум от 1win. Это не просто виртуальные симуляции покера в виде игровых автоматов из раздела онлайн казино. Нет, на сайте 1вин есть полноценный покер-рум с различными видыми покера, столами с лимитами и онлайн турнирами для участников. В этом разделе есть всё для действительно хорошей игры в покер.
Поскольку 1win сайт многоязычный и работает круглосуточно, то здесь вы всегда найдёте себе соперников со всего мира. Просто выбирайте свою любимую Омаху, или быть может Холдем или Техасский покер, садитесь за стол с подходящим уровнем соперников и вперёд к победе!

Еще одна причина присоединиться к нашему онлайн казино – это обширная бонусная программа. Интересные предложения откроют для себя как гэмблеры, так и бетторы. Предлагаем рассмотреть самые востребованные постоянные акции от нашей букмекерской конторы.

Помимо постоянных предложений, регулярно проводятся временные акции для всех зарегистрированных пользователей. Все актуальные бонусы 1win вы сможете найти, перейдя по ссылке, а сейчас вкратце расскажем о самых популярных.
Многие фанаты гемблинга любят начинать свой путь в онлайн казино с вкусного бонуса на депозит, чтобы попробовать как можно больше разных игр. 1win решили сделать так, чтобы каждый мог урвать сочную акцию для себя сразу же после регистрации.
Создавайте аккаунт, пополняйте баланс и получайте до 500% бонусом к вашему депозиту, с которыми вам будут открыты все двери на 1vin. После получения вам нужно будет их отыграть
Не стоит забывать, что выигрыши в слотах – это ваше везение и иногда оно подводит, но это совсем не повод расстраиваться, ведь 1win официальный сайт придет на выручку и тут! Хотите вернуть часть средств, которые успели проиграть – акция с кешбеком уже ждет вас.
Получите до 30% от утраченных средств в разделе «1win слоты» на свой баланс, попытайте удачу еще раз и она вам обязательно улыбнется!
Вы думали, что бонусы закончились? А вот и нет! Не забываем про программу лояльности 1vin, которую так любят игроки. В чем суть? Все просто: за каждую игру в разделе «Казино» вы получаете 1win coins, которые в дальнейшем можете обменять на реальные деньги и это очень помогает не только новичкам, но и опытным игрокам, исходя из опыта.
Важно отметить, что пари, которые заключены в Live Casino, в Баккаре, Покере, Рулетке и Блекджеке – не пойдут в зачет и монетки за них получить не выйдет. Но любые другие ставки пойдут в зачет, что крайне положительно скажется на вашем дальнейшем проценте побед, ведь всегда приятно получить даже небольшой, но бонус, с которым можно выиграть реально хорошие деньги на 1win!
Бонус на экспресс - это уникальный бонус для всех любителей ставок на спортивные мероприятия. При оформление экспресса с пятью и более событиями БК 1вин начислит вам дополнительный процент от выигрыша. Сам процент зависит от количества спортивных событий в экспрессе.
| Количество событий | Бонусный процент |
|---|---|
| 5 | 7% |
| 6 | 8% |
| 7 | 9% |
| 8 | 10% |
| 9 | 11% |
| 10 | 12% |
| 11+ | 15% |
Предпочитаете мобильный геймплей? Тогда установите официальное приложение платформы на свое устройство. Оно подходит на все современные смартфоны и планшеты. Предназначено для операционных систем Андроид и IOS.
Найти его просто. Прокрутите вниз главную страницу сайта прямо до футера. В нижней правой части интерфейса расположены иконки различных операционных систем, а именно: IOS, Android Windows. Нажмите на логотип вашего девайса, чтобы запустить автоматическое скачивания. А для авторизации используйте уже существующие логин и пароль.
Играть в 1 win casino с мобильного телефона – это не только невероятно удобно, но и выгодно. Вы наверняка не знали, что 1 вин предоставляют бонус за установку их приложения абсолютно каждому пользователю, который сделал это впервые. На ваш бонусный счет придут до 4000 гривен, которые вы можете отыграть, а затем вывести на основной баланс.
Условия отыгрыша крайне простые и не создадут вам никаких проблем, вы сможете просто наслаждаться геймплеем в онлайн казино 1win, отыгрывая бонус, разве это не круто?
Выбор нашего онлайн казино оправдан, в первую очередь, благодаря созданной нами удобной системе, призванной удовлетворить как гемблеров, так и бетторов. Оба типа игроков наслаждаются вниманием и щедрыми бонусами. Присоединение к платформе и выигрыш приза - процесс простой. Выигранные средства можно легко вывести на свой кошелек, воспользовавшись разнообразными платежными системами. Таким образом, 1вин не только обеспечивает надежную игровую среду, но также предлагает оптимальные условия и высокий уровень обслуживания.
И это только часть причин, почему вам стоит зарегистрироваться на официальном сайте нашего онлайн казино.
Чтобы иметь возможность пользоваться всеми прелестями сайта 1 casino win, вам необходимо скачала пройти процедуру регистрации. В 1win регистрация через официальный сайт невероятно простая и не займёт у вас более минуты, а в некоторых моментах и менее десяти секунд.
Последний способ рекомендуем для тех кто еще не определился с букмекерским сайтом, а быстрая регистрация поможет вам понять, что 1win - это то, что вам нужно!
Кроме этого, когда проходит в 1win казино регистрация, вы модете указать промокод, если он у вас есть. Такой промокод даст вам возможность получить больше бонусов. После завершения регистрации вы попадаете в свой личный кабинет, где можете сразу пополнить счёт или перейти к играм и попробовать поиграть в демо режиме уже в значительно большее количество игровых автоматов. Отметим, что часть игр в 1win казино даже в демо режиме доступно только зарегистрированным пользователям.
Рабочее зеркало 1win online дает доступ к официальному ресурсу, где сохраняются все данные клиента, в том числе деньги на балансе. Альтернативная версия создана с целью перенаправления пользователя на официальный сайт 1win pro в том случае, если доступ к нему по тем или иным причинам заблокирован.
Зеркало Ван Вин дает возможность пользоваться теми же опциями, которые есть на официальном ресурсе. Таким образом клиент может проводить финансовые операции, делать ставки на спорт, играть в казино, получать бонусы, принимать участие в турнирах и прочих акциях.
Для входа нужно открыть рабочее зеркало, ввести логин и пароль от учетной записи, после чего доступ к учетной записи будет открыт. Не рекомендуется использовать посторонние ресурсы, которые могут быть представлены как зеркало 1вин. Есть риск попасть на сайт мошенников, которые используют доверчивость неопытных игроков.
Также, ссылку на рабочее зеркало может предоставить служба техподдержки. Для этого нужно перейти на официальный сайт 1вин и запросить альтернативную версию площадки. Однако самый просттой способ перейти на зеркало 1win — нажать клавишу «Перейти на 1win» в верхнем меню текущего сайта!
Осуществить на сайте 1win вход очень просто, а главное - сделать это можно множеством различных способов. Первым делом необходимо зайти на 1 win официальный сайт и нажать на кнопку «1win войти». После чего в появившемся окне выбрать удобный для вас способ авторизации, например:
При клике на любую социальную сеть, вы будете перенаправлены на офсайт социальной сети, где вам необходимо будет выполнить вход в свой личный аккаунт. В этот момент вы автоматически вернётесь на 1 вин официальный сайт уже в качестве авторизованного игрока. Также можно вести электронную почту или телефон и пароль.
Если вы вдруг забыли, потеряли или просто не сохранили свой пароль после регистрации, его легко можно восстановить, нажав на надпись «Забыли пароль?», которая находится сразу под полем для ввода пароля. Если вы всё помните, тогда нажимаете кнопку «Продолжить» и радуетесь всем возможностям, которые получают беттеры и гемблеры, выполнившие на 1win сайт вход в личный кабинет.
Персональная учетная запись 1win online является личным кабинетом пользователя, где проводятся основные операции и выполняются любые действия.
Личный кабинет на Ван Вин дает возможность просматривать историю ставок пользователя, и хранит всю информацию о клиенте.
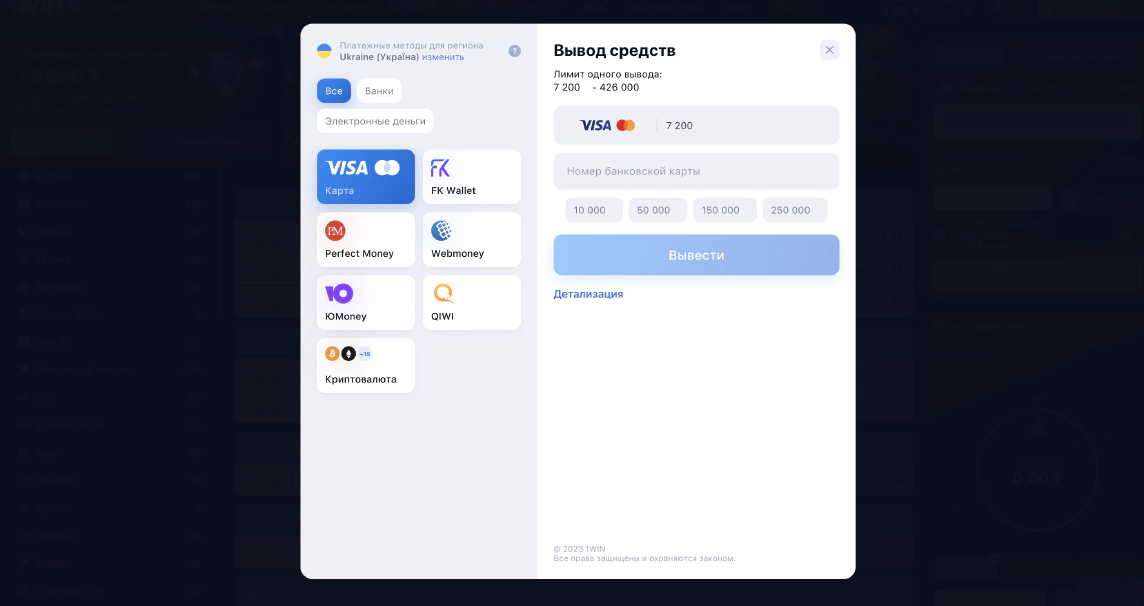
Ни у кого из клиентов компании 1вин не возникает проблем с выводом средств - вывести свой выигрыш вы сможете в любое время. Деньги всегда выводятся очень быстро и в полном объёме. Единственное, что для этого предварительно необходимо пройти верификацию. Такая процедура необходима для того, чтобы обезопасить все ваши денежные транзакции, обеспечить защиту ваших личных данных и в целом убедиться, что вы действительно человек и тот, за кого себя выдаёте.
Процедура вывода средств очень простая. Мы представили вам множество способов для совершения транзакций: платежные кошельки, кредитные и дебетовые карты, онлайн банкинг и даже криптовалюта! Выбирайте максимально комфортный для себя способ вывода.
При возникновении любых вопросов, по поводу вывода средств на свой счет — вы можете смело обратится в службу поддержки 1win. Наши специалисты работают на сайте 1 вин в режиме 24/7. Это сделано специально для того, чтобы сделать ваше присутствие на сайте и сам процесс игры более комфортным. Более того, на 1win офсайт присутствует максимально подробная инструкция, в которой до мельчайших деталей описан процесс вывода средств на каждый из доступных кошельков.
Кроме всего прочего, для того чтобы на нашем сайте не играли беттеры и гемблеры младше 18 лет, 1win официальный сайт регулярно проводит верификацию новых игроков. Чаще всего верификацию проходят перед первым выводом денежных средств, поэтому не стоит стараться обмануть систему. Лучше просто играть честно и соблюдать правила казино 1win.
Каждый, кто имел дело с казино онлайн понимает, насколько важна помощь со стороны администрации на любом этапе взаимодействия с порталом. Наличие качественной техподдержки всегда добавляет лишний плюс казино, поскольку пользователи часто обращают внимание на этот аспект при выборе конторы.
Компания 1 вин предлагает качественную техподдержку и работает 24/7, что является большим преимуществом, ведь клиенты проявляют активность на сайте в разное время суток в любой день недели.
В среднем работник отвечает в течение 8 минут. Время получения ответа на запрос может меняться в зависимости от выбранного способа обращения.
Поскольку скорость и качество - основные критерии оценки работы техподдержки, 1win официальный сайт старается максимально приближаться к идеалу.
Букмекерская контора 1win успешно оказывает свои услуги с 2016-го года, подтверждая свое лидерство на деле, а не только словах. Благодаря эффективной работе нашей команды в отзывах о нас трудно найти негативные мнения. Более 10 миллионов игроков уже выбрали 1win, получая максимальный комфорт для успешной игры.
1вин гарантирует своевременные выплаты выигрышей и предоставляет возможность превратить игру в источник дополнительного дохода. Таким образом, клуб 1-win становится отличным местом для увлекательного времяпровождения. Поэтому полагаясь на нас, вы получите оптимальные условия для азартных игр и ставок.
Букмекерская контора 1vin — это лицензированная площадка с азартными развлечениями. Заведение имеет лицензию на проведение азартных игр формата: №8048/JAZ2018-040 Antillephone N.V. (Curacao). Это означает, что все азартные игры являются лицензированными, поэтому вам не стоит переживать за процент отдачи слотов онлайн. Поэтому вам не придется переживать за выплаты и сохранность личной информации. Лицензия — это гарант и защита! Сделайте правильный выбор и зарегистрируйтесь в казино 1win!

Для игры проверь VPN
Олег
Курбатов Олег, Буча 03.02.2021
Юрий
Юрий В., Харьков, 13.08.2020
Horrow_shiy
Horrow_shiy, Луцк, 22.01.2021
Разговорчивый
Разговорчивый, Умань, 11.07.2021
Олег К.
Олег К., Миргород, Июнь 2019